I couldn’t answer that question myself for a long time. I thought “Hey both signals travel at the same speed of light, why is there a difference?”. So I wrote this memo to myself (and maybe others) trying to answer that question once and for all.
The Doppler effect, which is the change in frequency or wavelength of a wave in relation to an observer moving relative to the wave source, is more pronounced at higher frequencies. This is why it’s more significant when using the 70 cm band (approximately 420-450 MHz) for space communications compared to the 2 m band (approximately 144-148 MHz).
Here are the main reasons why the Doppler effect impacts the 70 cm band more than the 2 m band:
- Frequency Proportionality: The Doppler shift is directly proportional to the frequency of the transmitted signal. Higher frequencies experience greater Doppler shifts. Since the 70 cm band operates at around 430 MHz and the 2 m band at around 145 MHz, the Doppler shift is more noticeable on the 70 cm band. Specifically, for the same relative velocity between the transmitter and receiver, the Doppler shift on the 70 cm band will be about three times greater than that on the 2 m band.
- Space Communications Dynamics: Satellites and space stations move at high velocities relative to the Earth. For low Earth orbit (LEO) satellites, velocities can be in the range of 7-8 km/s. At such speeds, the Doppler shift can be several kHz for the 70 cm band, which can cause significant issues in maintaining a stable communication link without compensating for the frequency shift. In contrast, while the 2 m band also experiences a Doppler shift, it is less severe (only about one-third as much), and thus less problematic.
- Signal Processing and Bandwidth: The relative bandwidth of signals in these bands also matters. In the 70 cm band, the percentage change in frequency due to Doppler shift is more significant compared to the signal bandwidth than it is in the 2 m band. Therefore, the effect on communication quality and the need for Doppler correction are more critical at higher frequencies.
Mathematical approach
This mathematical comparison illustrates why the Doppler effect is more significant for communications in the 70 cm band compared to the 2 m band and shows how we can calculate the Doppler shift using the formula

where:
- v is the relative velocity between the source and the observer,
- c is the speed of light (≈3×108 m/s),
- f0 is the original frequency of the transmitted signal.
Let’s denote the frequencies for the 2 m and 70 cm bands as f 2m and f 70cm, respectively.
For the 2 m band (around 145 MHz):

For the 70 cm band (around 430 MHz):

The Doppler shift for each band can be expressed as:
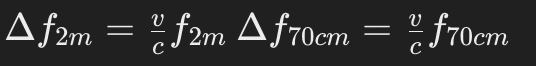
Since the Doppler shift is directly proportional to the frequency, the ratio of the Doppler shifts for the two bands is given by:
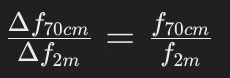
Substituting the frequencies:
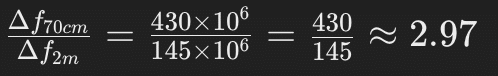
Therefore, the Doppler shift for the 70 cm band is approximately 2.97 times greater than the Doppler shift for the 2m band for the same relative velocity v.
Logical approach:
On the 2m band, the the transmission of a payload, say “CQ ISS DO8YDP” takes only a few full wave circles, let’s say 100.
While on the 70cm band, the same words, same transmission, same payloads needs three times the amount of full wave cycles in this calculation 300, exposing every single wave to vulnerability to the Doppler effect.
So you can imagine the Doppler effect changing every frequency by the same percentage. Physically you have to adjust on both bands but you can get away without it on 2m. A 0.0056% increase at 145.000 MHz is 145.008 MHz, but it changes 440.000 MHz to 440.025 MHz. So on 440 MHz this would carry the signal straight out of your receivers frequency range, while it wouldn’t on 2m – you would just loose a very small of receiving signal when the satellite or ISS is very close to the horizon.
My math and physics teachers would be so proud of me. Mr. Wichmann and Mr. Waschescio, you proud now?