Warum wird der Dopplereffekt auf dem 70-cm-Band (435 MHz), aber nicht auf dem 2-m-Band (145 MHz) beim Satellitenbetrieb oder der Weltraumkommunikation berücksichtigt?

Ich selbst konnte diese Frage lange Zeit nicht beantworten. Ich dachte: „Hey, beide Signale bewegen sich mit derselben Lichtgeschwindigkeit, warum gibt es da einen Unterschied?“. Also schrieb ich dieses Memo an mich selbst (und vielleicht auch an andere), um diese Frage ein für alle Mal zu beantworten.

Der Dopplereffekt, d. h. die Änderung der Frequenz oder Wellenlänge einer Welle in Bezug auf einen Beobachter, der sich relativ zur Wellenquelle bewegt, ist bei höheren Frequenzen stärker ausgeprägt. Aus diesem Grund ist er bei der Nutzung des 70-cm-Bands (ca. 420-450 MHz) für die Weltraumkommunikation stärker ausgeprägt als beim 2-m-Band (ca. 144-148 MHz).

Hier sind die Hauptgründe, warum der Dopplereffekt auf dem 70-cm-Band stärker wirkt als auf dem 2-m-Band:

1. Frequenzproportionalität: Die Doppler-Verschiebung ist direkt proportional zur Frequenz des übertragenen Signals. Bei höheren Frequenzen ist die Dopplerverschiebung größer. Da das 70-cm-Band bei etwa 430 MHz und das 2-m-Band bei etwa 145 MHz arbeitet, ist die Dopplerverschiebung auf dem 70-cm-Band stärker ausgeprägt. Bei gleicher Relativgeschwindigkeit zwischen Sender und Empfänger ist die Dopplerverschiebung auf dem 70-cm-Band etwa dreimal so groß wie auf dem 2-m-Band.
2. Dynamik der Weltraumkommunikation: Satelliten und Raumstationen bewegen sich mit hohen Geschwindigkeiten relativ zur Erde. Bei Satelliten in einer niedrigen Erdumlaufbahn (LEO) können die Geschwindigkeiten im Bereich von 7-8 km/s liegen. Bei solchen Geschwindigkeiten kann die Dopplerverschiebung im 70-cm-Band mehrere kHz betragen, was ohne Kompensation der Frequenzverschiebung zu erheblichen Problemen bei der Aufrechterhaltung einer stabilen Kommunikationsverbindung führen kann. Im Gegensatz dazu ist die Dopplerverschiebung im 2-m-Band zwar auch vorhanden, aber weniger stark (nur etwa ein Drittel) und daher weniger problematisch.
3. Signalverarbeitung und Bandbreite: Die relative Bandbreite der Signale in diesen Bändern spielt ebenfalls eine Rolle. Im 70-cm-Band ist die prozentuale Frequenzänderung aufgrund der Dopplerverschiebung im Vergleich zur Signalbandbreite bedeutender als im 2-m-Band. Daher sind die Auswirkungen auf die Kommunikationsqualität und die Notwendigkeit einer Dopplerkorrektur bei höheren Frequenzen kritischer.
   

Mathematischer Ansatz

Dieser mathematische Vergleich veranschaulicht, warum der Dopplereffekt für die Kommunikation im 70-cm-Band bedeutender ist als im 2-m-Band, und zeigt, wie man die Dopplerverschiebung mit der folgenden Formel berechnen kann

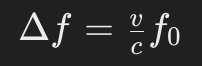
wobei

• v die relative Geschwindigkeit zwischen der Quelle und dem Beobachter ist,
• c die Lichtgeschwindigkeit ist (≈3×10⁸ m/s),
• f0 die ursprüngliche Frequenz des übertragenen Signals ist.

Bezeichnen wir die Frequenzen für das 2-m- und das 70-cm-Band als  und ​.

Für das 2-m-Band (um 145 MHz):  

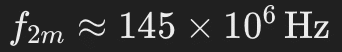
Für das 70-cm-Band (etwa 430 MHz): 

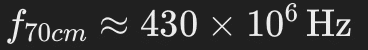
Die Dopplerverschiebung für jedes Band kann wie folgt ausgedrückt werden:

_oder

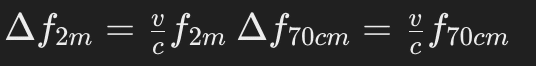
Da die Dopplerverschiebung direkt proportional zur Frequenz ist, ergibt sich das Verhältnis der Dopplerverschiebungen für die beiden Bänder wie folgt:

Einsetzen der Frequenzen:

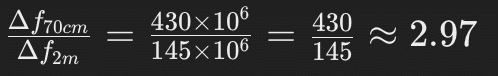
Daher ist die Dopplerverschiebung für das 70-cm-Band etwa 2,97-mal größer als die Dopplerverschiebung für das 2-m-Band bei gleicher Relativgeschwindigkeit v.

Logischer Ansatz:

Auf dem 2-m-Band dauert die Übertragung einer Nutzlast, z. B. „CQ ISS DO8YDP“, nur wenige Vollwellendurchläufe, sagen wir stark vereinfact 100.
Auf dem 70-cm-Band hingegen sind für die gleichen Worte, die gleiche Übertragung und die gleiche Nutzlast dreimal so viele Vollwellendurchläufe erforderlich, in diesem Fall 300, wodurch jede einzelne Welle dem Dopplereffekt ausgesetzt ist, was sich bei 300 statt 100 Wellen deimal so stark auswirkt.

Man kann sich also vorstellen, dass der Dopplereffekt jede Frequenz um den gleichen Prozentsatz verändert. Physikalisch muss man auf beiden Bändern nachregeln, aber auf 2m kann man darauf verzichten. Eine Erhöhung um 0,0056% bei 145,000 MHz ist 145,008 MHz, aber 440,000 MHz wird dadurch zu 440,025 MHz. Auf 440 MHz würde das Signal also direkt aus dem Frequenzbereich des Empfängers hinausgetragen werden, während das auf 2m nicht der Fall wäre – man würde nur einen sehr kleinen Teil des Empfangssignals verlieren, wenn der Satellit oder die ISS sehr nahe am Horizont ist.

Meine Mathe- und Physiklehrer wären stolz auf mich. Herr Wichmann und Herr Waschescio, was sagen Sie nun?